Spiral Nedir?Spiral, matematiksel bir kavram olarak, bir noktadan başlayarak belirli bir merkez etrafında dönen ve giderek uzaklaşan bir eğridir. Geometrik olarak, spiral eğrileri iki temel türde incelenebilir: Arşimed spirali ve logaritmik spirali. Arşimed spirali, eşit aralıklarla genişleyen bir yapıya sahipken, logaritmik spiral, her turda belirli bir oranla genişler ve doğal dünyada birçok yerde karşımıza çıkar. Spiral ÇeşitleriSpiral, matematik ve geometri alanlarında çeşitli türlerde incelenmektedir. Bu türler arasında en yaygın olanları şunlardır:
Her bir spiral türü, farklı matematiksel formüller ve özellikler içerir. Arşimed spirali, \( r = a + b\theta \) formülüyle tanımlanırken, logaritmik spiral \( r = ae^{b\theta} \) formülüyle ifade edilir. Fibonacci spirali ise Fibonacci sayılarına dayanmaktadır ve doğal düzenleri simgeler. Spiralin Kullanım AlanlarıSpiral, birçok farklı alanda uygulama bulmaktadır. İşte bazı önemli kullanım alanları:
Bu alanlar, spiral kavramının çok yönlü doğasını ve çeşitli disiplinlerde nasıl yer bulduğunu göstermektedir. Spiral ve DoğaSpiral biçimleri, doğada sıkça gözlemlenen bir fenomendir. Özellikle bitkiler, hayvanlar ve doğal oluşumlar arasında spirallere rastlamak mümkündür. Örneğin:
Bu tür örnekler, doğanın matematikle olan ilişkisinin ne denli derin olduğunu ortaya koymaktadır. SonuçSpiral, matematiksel bir kavram olmanın ötesinde, doğada ve insan yapımı yapılar içinde önemli bir yer tutmaktadır. Matematikten sanata, mühendislikten tıbba kadar geniş bir yelpazede kullanım alanı bulan spiraller, hem estetik hem de işlevsel açıdan değer taşımaktadır. Bu çok yönlülük, spiral kavramının neden bu kadar önemli olduğunu ve çeşitli disiplinlerde nasıl değerlendirildiğini açıkça göstermektedir. |
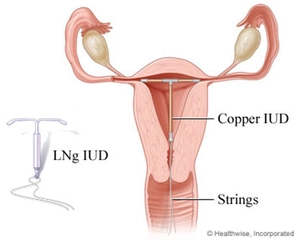
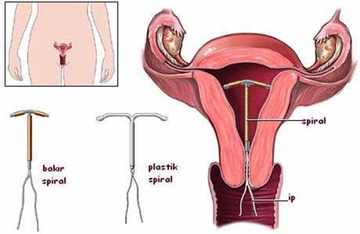
Spiral kavramı gerçekten de doğada ve matematikteki yerini çok iyi yansıtıyor. Özellikle doğada gördüğümüz spiral formlar, bu kavramın ne kadar yaygın olduğunu gösteriyor. Fıstık çamı ve ayçiçeği gibi bitkilerin tohum düzenleri gerçekten de ilginç. Bu tür örneklerin yanı sıra logaritmik spirallerin deniz kabuklarında nasıl büyüdüğünü görmek de doğanın harika bir tasarımı değil mi? Spirallerin sanat ve mimarideki kullanımı da estetik açıdan oldukça etkileyici. Matematiksel formüllerin arkasındaki derinliği düşününce, spiralin hem işlevsel hem de görsel açıdan neden bu kadar önemli olduğunu daha iyi anlıyoruz. Bu konudaki düşünceleriniz nelerdir?
Cevap yaz